8 Zusammenhänge in Daten erkennen

Bisher haben wir Daten vor allem einzeln beschrieben – durch Häufigkeiten, typische Werte oder ihre Streuung. Oft interessiert uns jedoch, wie zwei Variablen zusammenhängen:
„Steigt die Prüfungsleistung, wenn mehr gelernt wird?“
„Hängt das Einkommen mit der Berufserfahrung zusammen?“

Zur Untersuchung solcher Zusammenhänge gibt es verschiedene Werkzeuge, die im Folgenden vorgestellt werden.

Kovarianz

Bisher haben wir Streuung nur bei einer einzelnen Variablen betrachtet – mit Varianz und Standardabweichung.
Nun interessiert uns, ob zwei Variablen gemeinsam schwanken.

Beispiel:
- Steigt die Lernzeit, steigt auch die Prüfungsleistung?
- Oder: Wenn die eine Größe zunimmt, nimmt die andere ab?

Um das zu messen, verwenden wir die Kovarianz.

\[ \operatorname{Cov}(X,Y) = \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y}) \]

Interpretation:

\(\operatorname{Cov}(X,Y) > 0\): Beide Größen schwanken gemeinsam nach oben oder unten.
\(\operatorname{Cov}(X,Y) < 0\): Wenn die eine steigt, fällt die andere.
\(\operatorname{Cov}(X,Y) \approx 0\): Kein erkennbarer gemeinsamer Zusammenhang.

Die Kovarianz ist also eine Verallgemeinerung der Varianz:

Bei der Varianz multipliziert man die Abweichung einer Variablen mit sich selbst: \((x_i - \bar{x})^2\)
Bei der Kovarianz multipliziert man die Abweichungen zweier Variablen: \((x_i - \bar{x})(y_i - \bar{y})\)

Beispiel:
- Wenn längere Lernzeit meist auch zu besseren Prüfungsnoten führt, ist die Kovarianz positiv.
- Wenn längere Lernzeit paradoxerweise zu schlechteren Noten führen würde, wäre sie negativ.
- Wenn Lernzeit und Note nichts miteinander zu tun hätten, läge sie nahe bei null.

Aber: Die Kovarianz hängt von den Maßeinheiten der Daten ab (z. B. Stunden und Punkte).
Deshalb ist sie schwer zu interpretieren.

Dafür gibt es im nächsten Schritt den Pearson-Korrelationskoeffizienten:
eine normierte Kovarianz, die immer zwischen (-1) und (+1) liegt und speziell lineare Zusammenhänge beschreibt.

Lineare Zusammenhänge

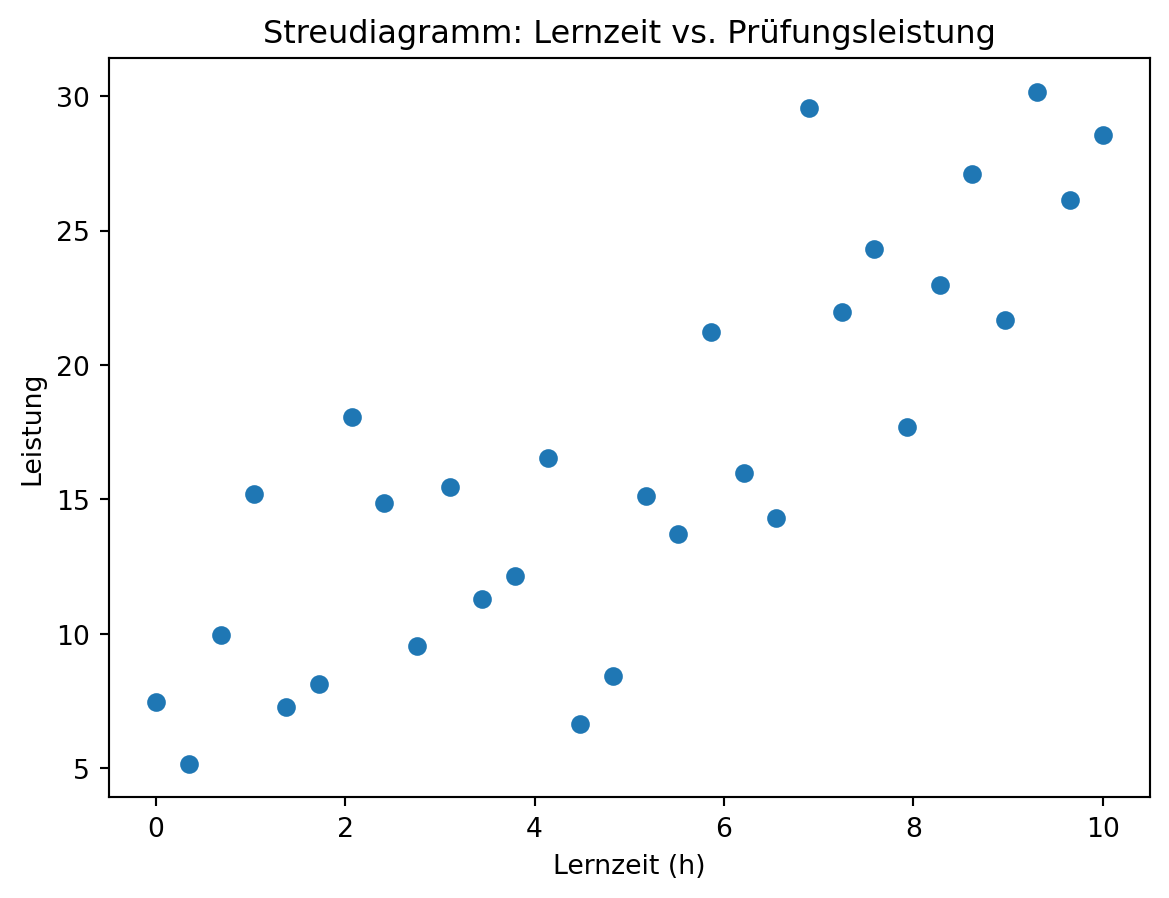
Ein erster Schritt ist die grafische Darstellung in einem Streudiagramm.
Sind die Punkte annähernd auf einer Geraden angeordnet, spricht man von einem linearen Zusammenhang.

Beispiel: Zusammenhang zwischen Lernzeit und Prüfungsnote.

Pearson-Korrelationskoeffizient

Der Korrelationskoeffizient nach Pearson misst die Stärke und Richtung eines linearen Zusammenhangs:

\[ r_{XY} = \frac{\operatorname{Cov}(X, Y)}{s_X \cdot s_Y} \]

Wir berechnen ihn allerdings meist ohne zuvor Kovarianz und Standardabweichungen zu ermitteln:

\[ r = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^n (x_i - \bar{x})^2 \cdot \sum_{i=1}^n (y_i - \bar{y})^2}} \]

\(r = +1\): perfekter positiver linearer Zusammenhang
\(r = -1\): perfekter negativer linearer Zusammenhang
\(r \approx 0\): kein linearer Zusammenhang

Korrelationskoeffizient r = 0.82

Übung: Rechnen Sie das Beispiel selbst nach!

x (Lernzeit)	y (Leistung)	x (Lernzeit)	y (Leistung)
0.00	7.48	5.17	15.12
0.34	5.17	5.52	13.73
0.69	9.96	5.86	21.23
1.03	15.20	6.21	15.98
1.38	7.28	6.55	14.32
1.72	8.14	6.90	29.57
2.07	18.07	7.24	21.97
2.41	14.87	7.59	24.30
2.76	9.55	7.93	17.70
3.10	15.47	8.28	22.97
3.45	11.30	8.62	27.11
3.79	12.15	8.97	21.66
4.14	16.55	9.31	30.15
4.48	6.64	9.66	26.13
4.83	8.44	10.00	28.54

Die Korrelationsmatrix ist ein nützliches Werkzeug, um in multidimensionalen Datensätzen alle paarweisen linearen Zusammenhänge auf einen Blick zu erfassen. Sie stellt den Korrelationskoeffizienten für jede Kombination von Variablen dar und ermöglicht so, Abhängigkeiten zu erkennen.

Beispiel: Wir ergänzen unseren Datensatz mit den Variablen Lernzeit und Leistung um eine dritte Variable Alter und stellen die Korrelationsmatrix mitsamt Heatmap auf.

Code

import seaborn as sns
import pandas as pd

# Beispiel-Daten
df = pd.DataFrame({
    "Lernzeit": x,
    "Leistung": y,
    "Alter": np.random.randint(15, 25, size=30)
})

sns.heatmap(df.corr(), annot=True, cmap="coolwarm", center=0)
plt.title("Korrelationsmatrix")
plt.show()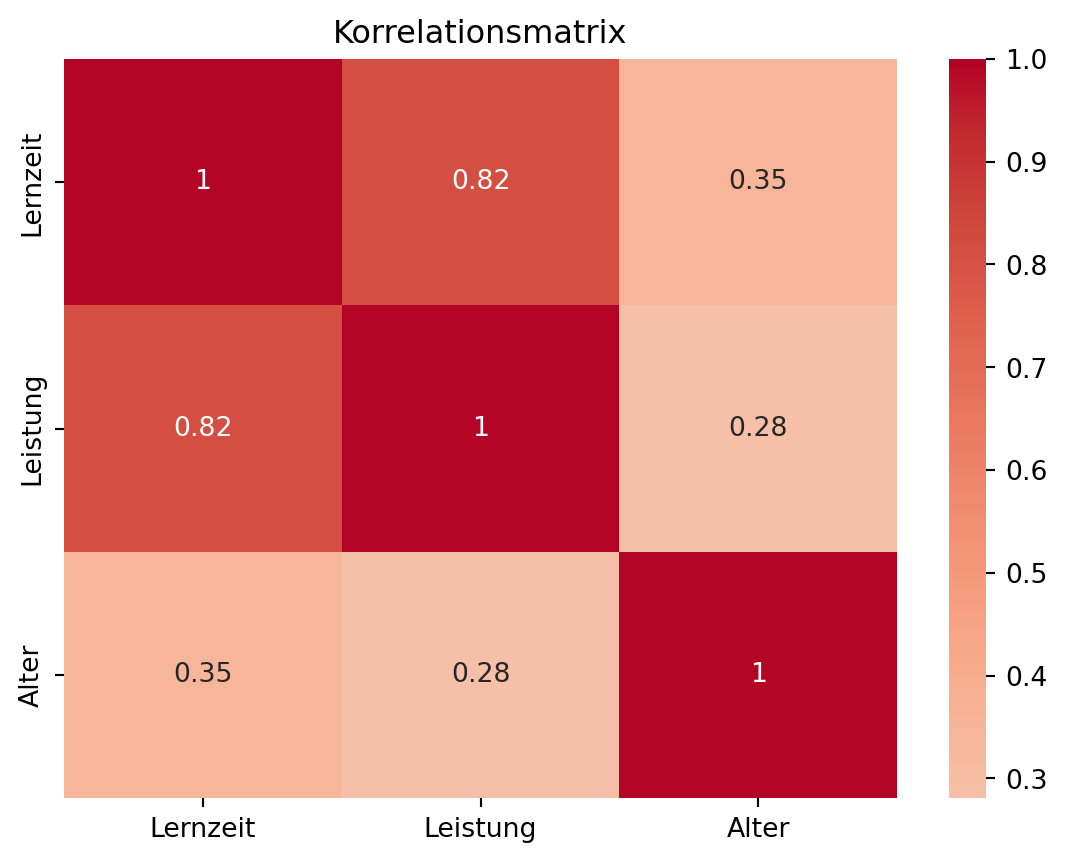

Achtung

Korrelation ist nicht Kausalität!

Ein hoher Korrelationskoeffizient bedeutet nicht automatisch, dass eine Variable die Ursache der anderen ist.

Beispiel:
Die Anzahl verkaufter Eiscremes und die Zahl der Ertrinkungsunfälle sind positiv korreliert – die eigentliche Ursache ist jedoch die Temperatur (Sommer).

Korrelation beschreibt also nur den statistischen Zusammenhang, nicht das Ursache-Wirkung-Verhältnis.

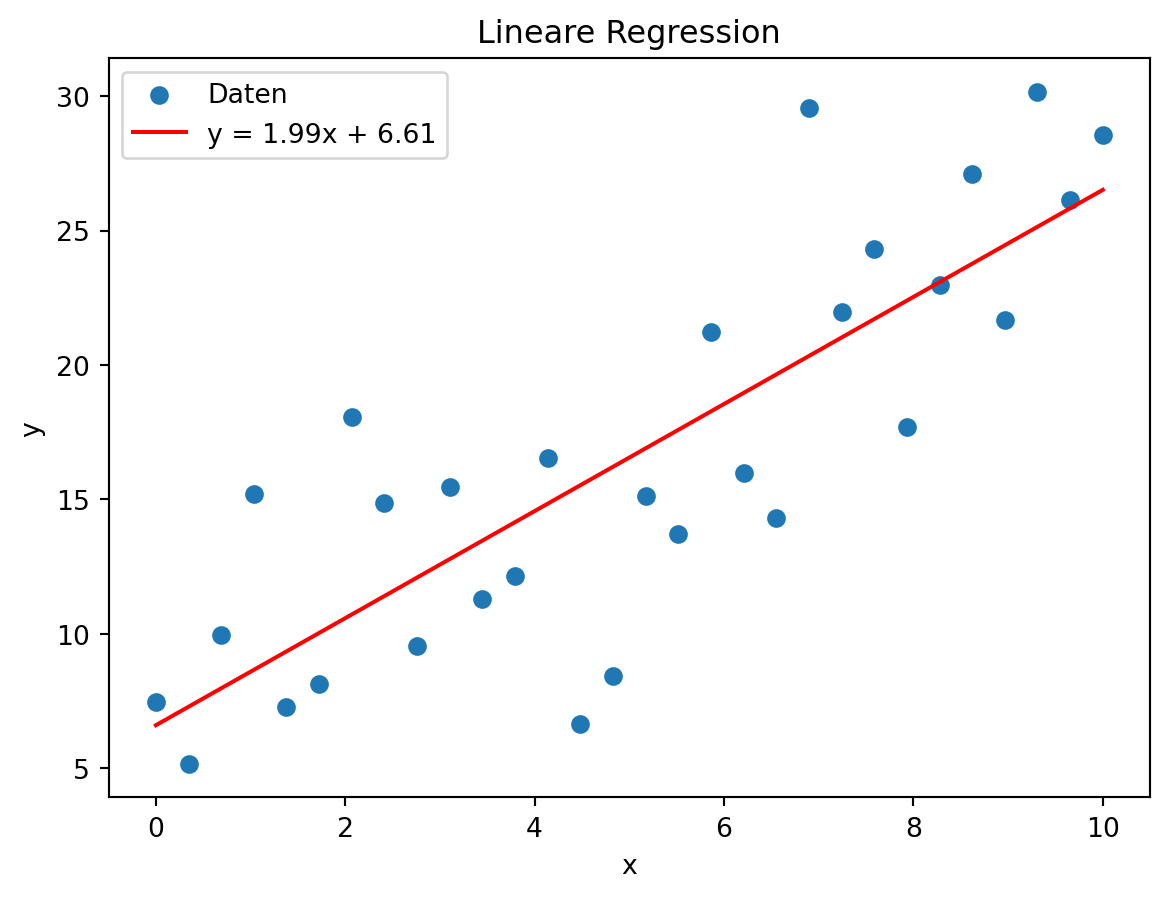
Regressionsgerade

Die lineare Regression findet eine Gerade, die den Zusammenhang zwischen den Datenpunkten optimal wiedergibt.
Die Gerade hat die Form:

\[ y = a \cdot x + b \]

Dabei werden \(a\) und \(b\) so gewählt, dass die Summe der quadrierten Abweichungen \(\sum (y_i - (a x_i + b))^2\) möglichst klein ist (Kleinste-Quadrate-Methode).

Die Steigung \(a\) berechnet sich: \[ a = \frac{\sum (x_i - \bar{x})(y_i - \bar{y})}{\sum (x_i - \bar{x})^2}, \] Der y-Achsenabschnitt \(b\) wird so berechnet:

\[ b = \bar{y} - a \cdot \bar{x} \]

Nichtlineare Zusammenhänge

Nicht alle Zusammenhänge sind linear. Manchmal folgt der Verlauf z. B. einer Quadratfunktion oder einer Exponentialfunktion.

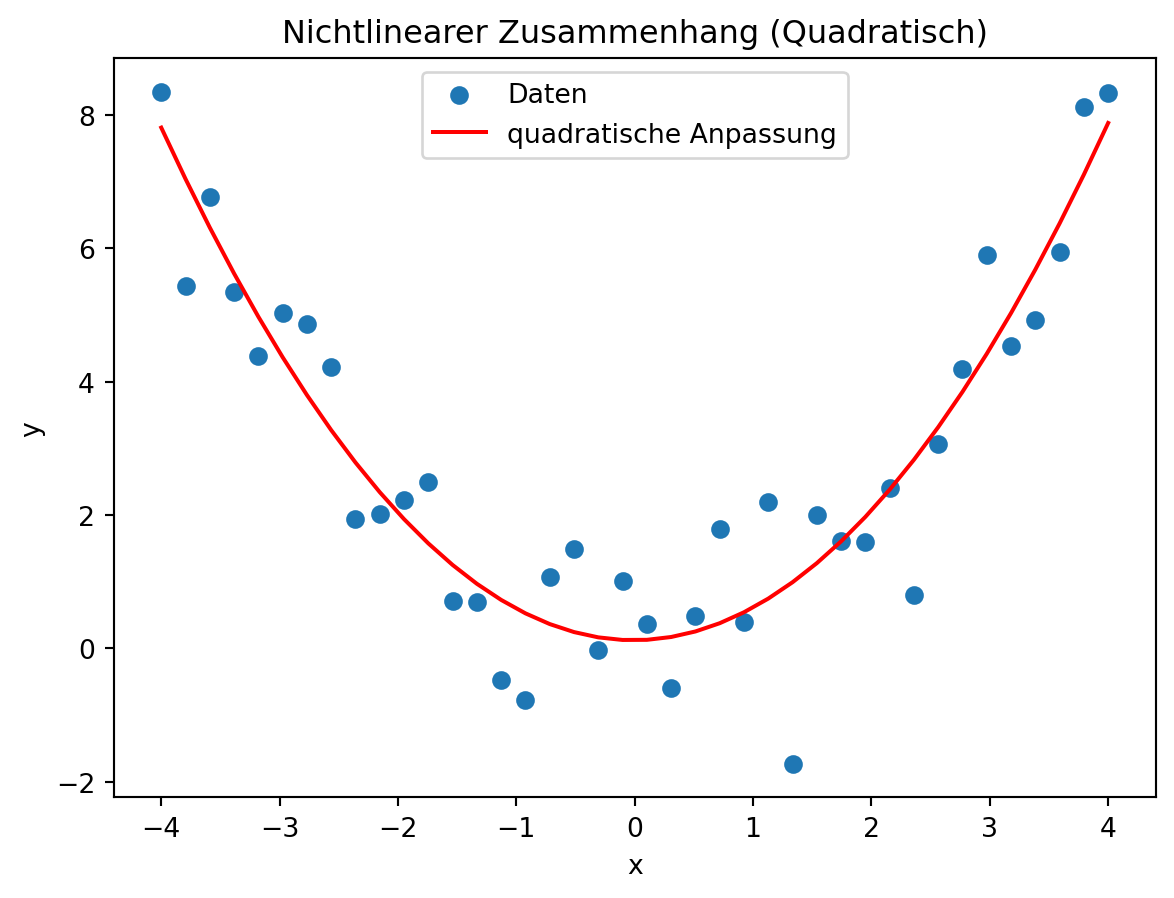
Quadratischer Zusammenhang

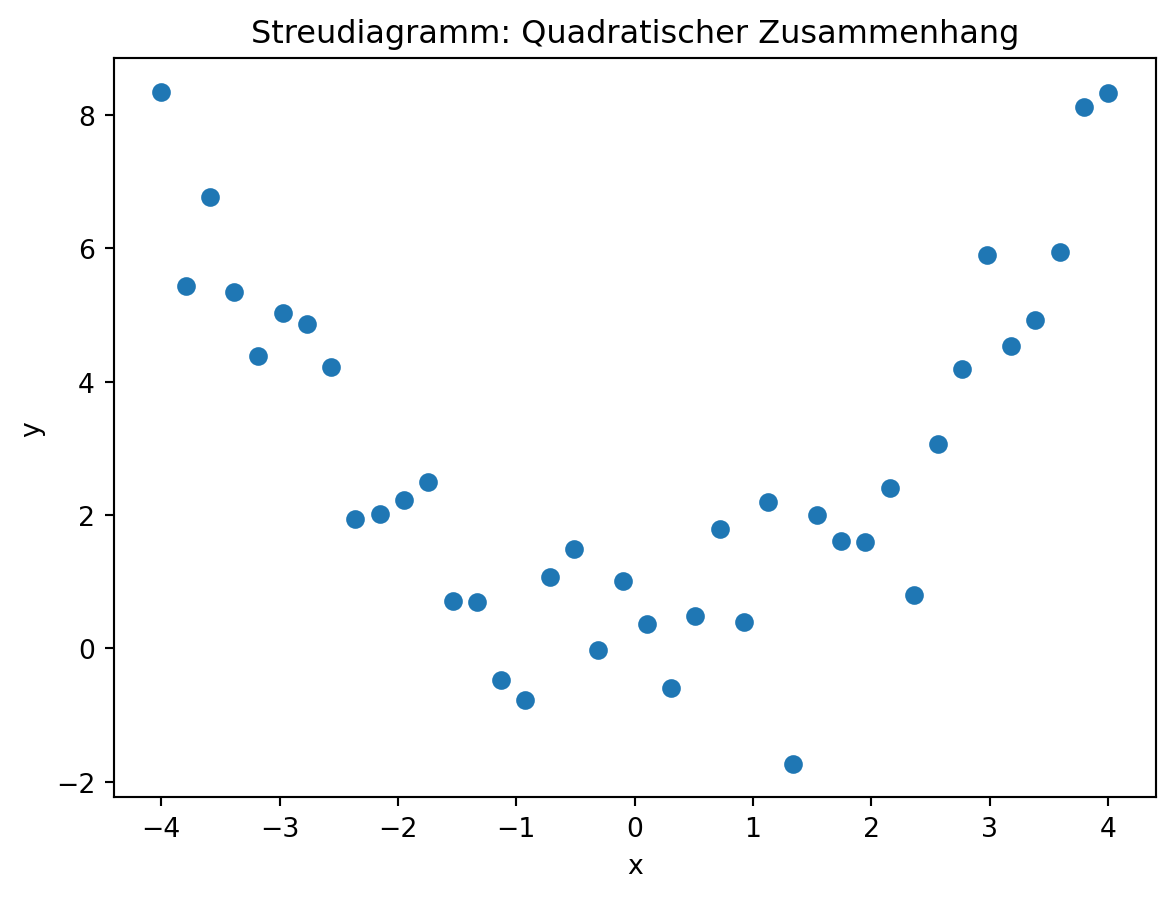
Auch hier lässt sich eine passende Funktion durch die Daten legen – man spricht allgemein von einer nichtlinearen Regression.

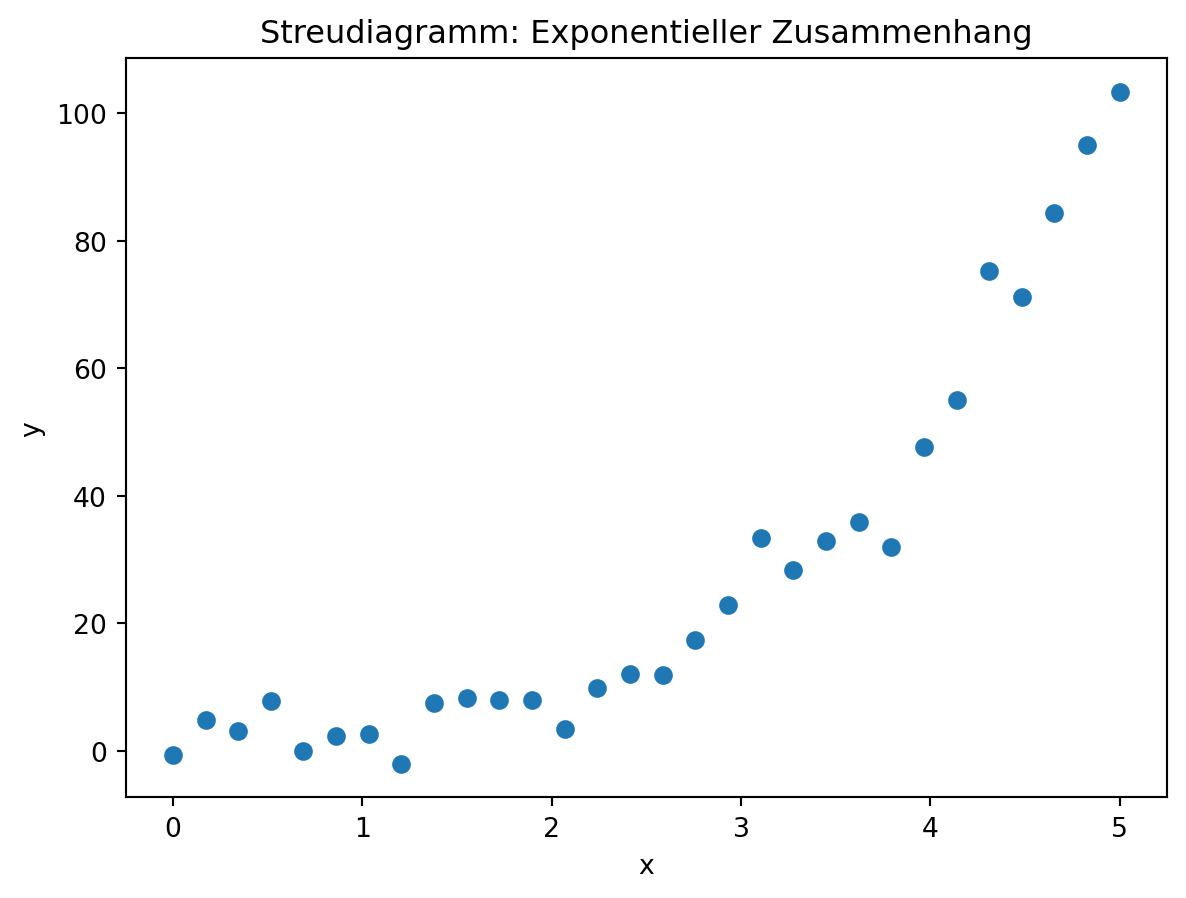
Exponentieller Zusammenhang

Ein weiteres Beispiel ist exponentielles Wachstum, wie man es etwa bei Bevölkerungszahlen oder Infektionsausbreitung beobachten kann.

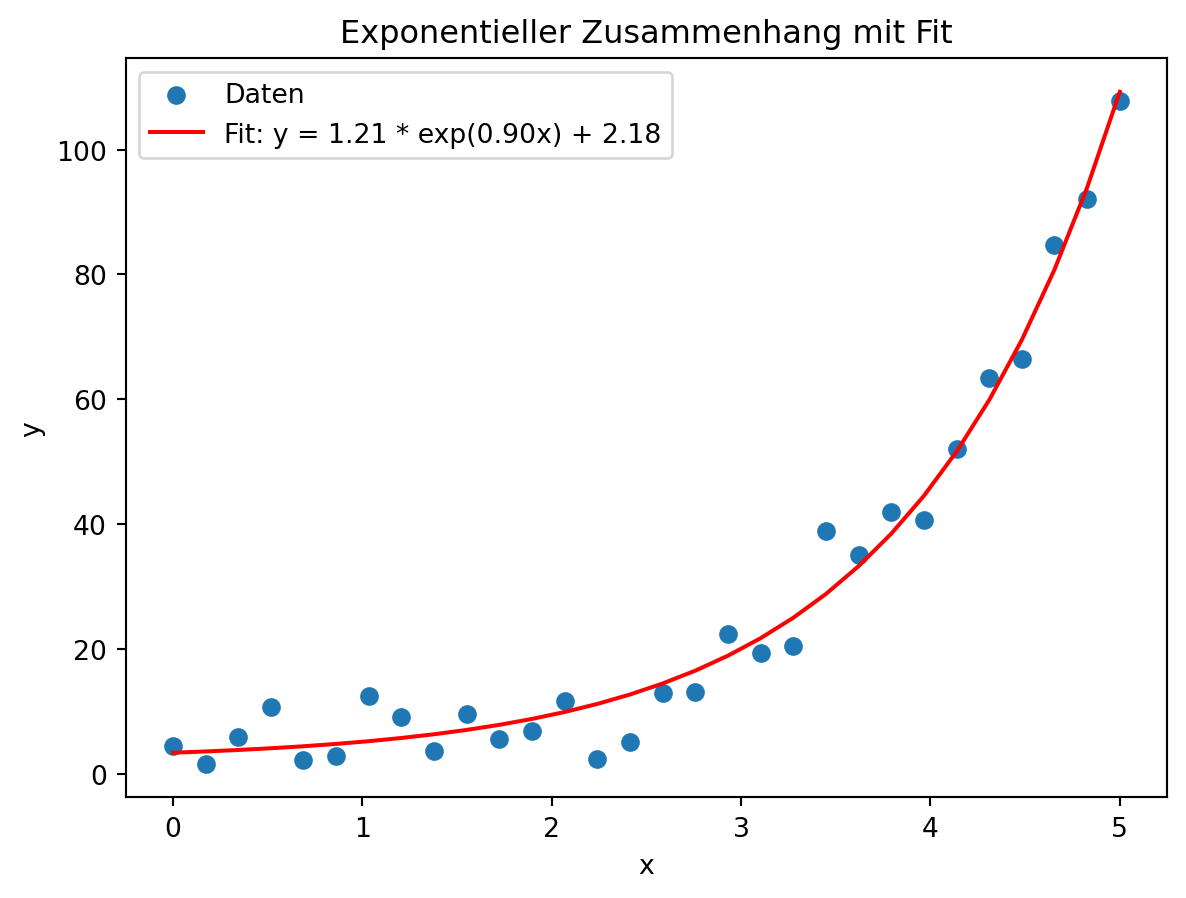
Fazit

Lineare Zusammenhänge lassen sich mit Streudiagrammen sichtbar machen, mit dem Korrelationskoeffizienten messen und mit einer Regressionsgeraden beschreiben. Auch nichtlineare Zusammenhänge können modelliert werden, wenn man ein passendes Modell (z. B. quadratisch oder exponentiell) wählt.

In der Praxis kennt man den zugrunde liegenden Zusammenhang jedoch oft nicht. Hier können Methoden des Maschinellen Lernens helfen, da sie in der Lage sind, komplexe Muster und Beziehungen in Daten automatisch zu erkennen.