7  Datenvisualisierung

Neben der tabellarischen Darstellung von Häufigkeiten, Lage- und Streuungsmaßen ist die grafische Aufbereitung von Daten ein zentrales Werkzeug der deskriptiven Statistik.
Visualisierungen machen Muster, Unterschiede und Auffälligkeiten oft auf den ersten Blick erkennbar und erleichtern das Verständnis komplexer Datensätze.

Je nach Skalenniveau und Fragestellung eignen sich unterschiedliche Diagrammtypen.

Grundprinzipien guter Visualisierung

• Klarheit: Die Darstellung sollte einfach verständlich sein und ohne unnötige Verzierung auskommen.
  
• Vergleichbarkeit: Werte sollen sich leicht vergleichen lassen.
  
• Angemessenheit: Der Diagrammtyp muss zur Art der Daten passen.
  
• Vollständigkeit: Wichtige Informationen (z. B. Achsenbeschriftungen, Legenden) dürfen nicht fehlen.

Häufigkeitsdiagramme

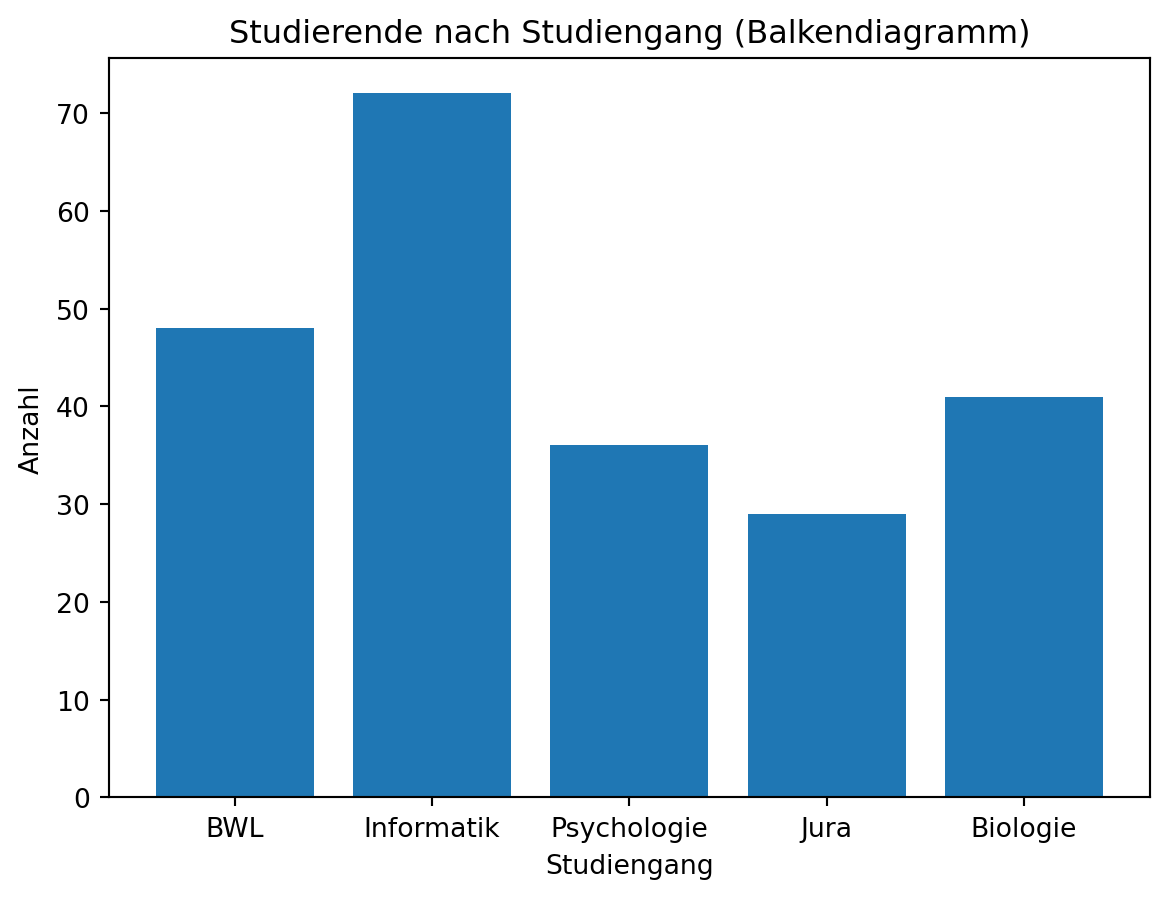
• Balkendiagramm (Bar Chart):
  Geeignet für nominale und ordinale Daten.
  Jeder Balken repräsentiert die Häufigkeit (absolut oder relativ) einer Kategorie.

  Beispiel: Die Anzahl der Studierenden in verschiedenen Studiengängen.

  

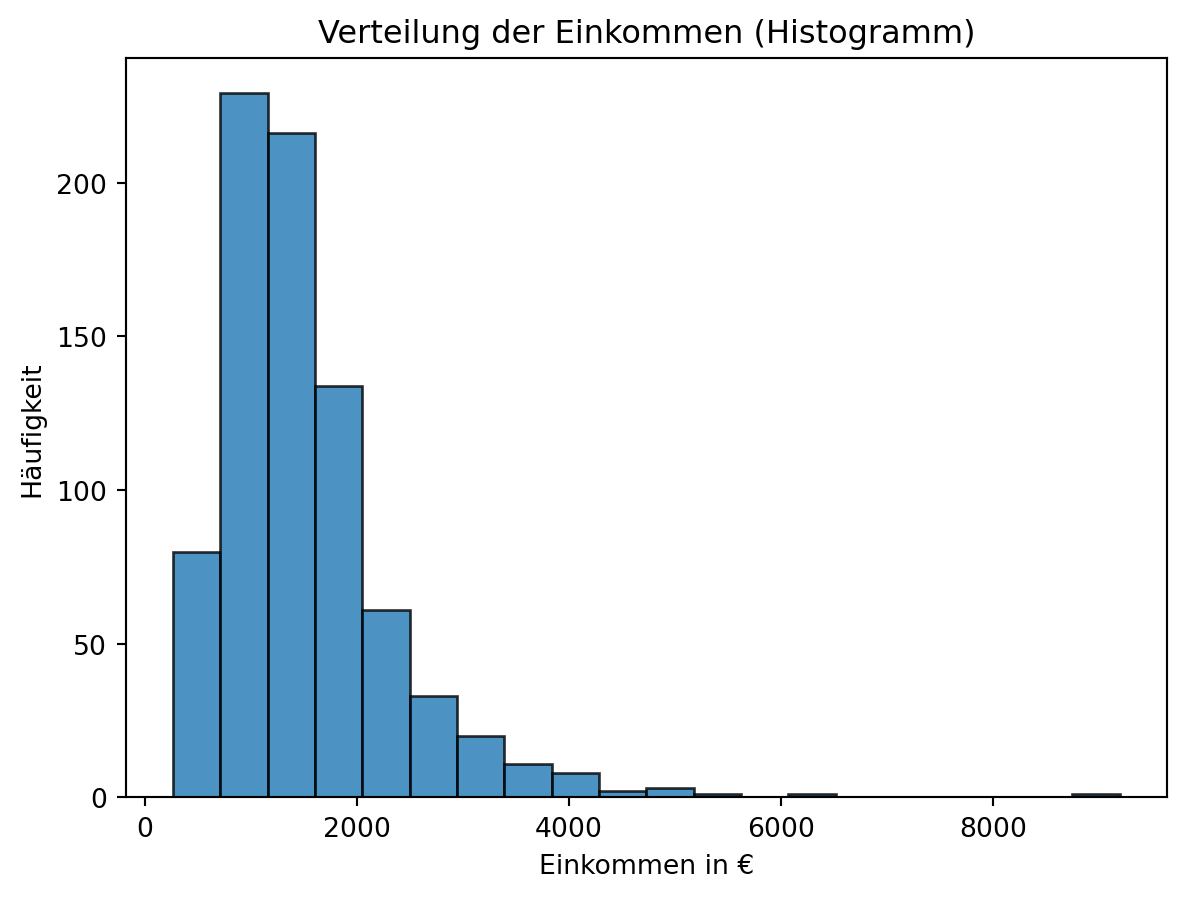
• Histogramm:
  Verwendet für metrische Daten, die in Klassenintervalle eingeteilt werden.
  Die Balken stehen direkt nebeneinander und zeigen die Häufigkeit in jedem Intervall.

  Beispiel: Verteilung der Einkommen in einer Befragung.

  

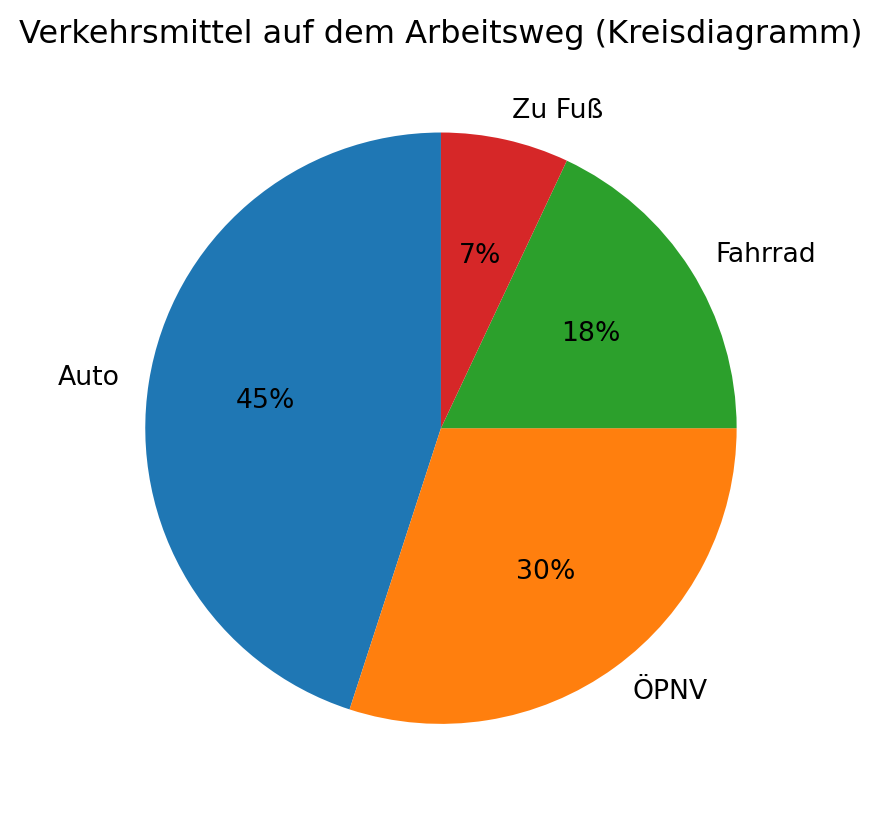
• Kreisdiagramm (Pie Chart):
  Stellt relative Häufigkeiten als Anteile eines Kreises dar.
  Eignet sich besonders für nominale Daten mit wenigen Kategorien.

  Beispiel: Anteil der Verkehrsmittel bei Arbeitswegen (Auto, Bahn, Fahrrad, …).

  

Lagemaße und Streuung grafisch darstellen

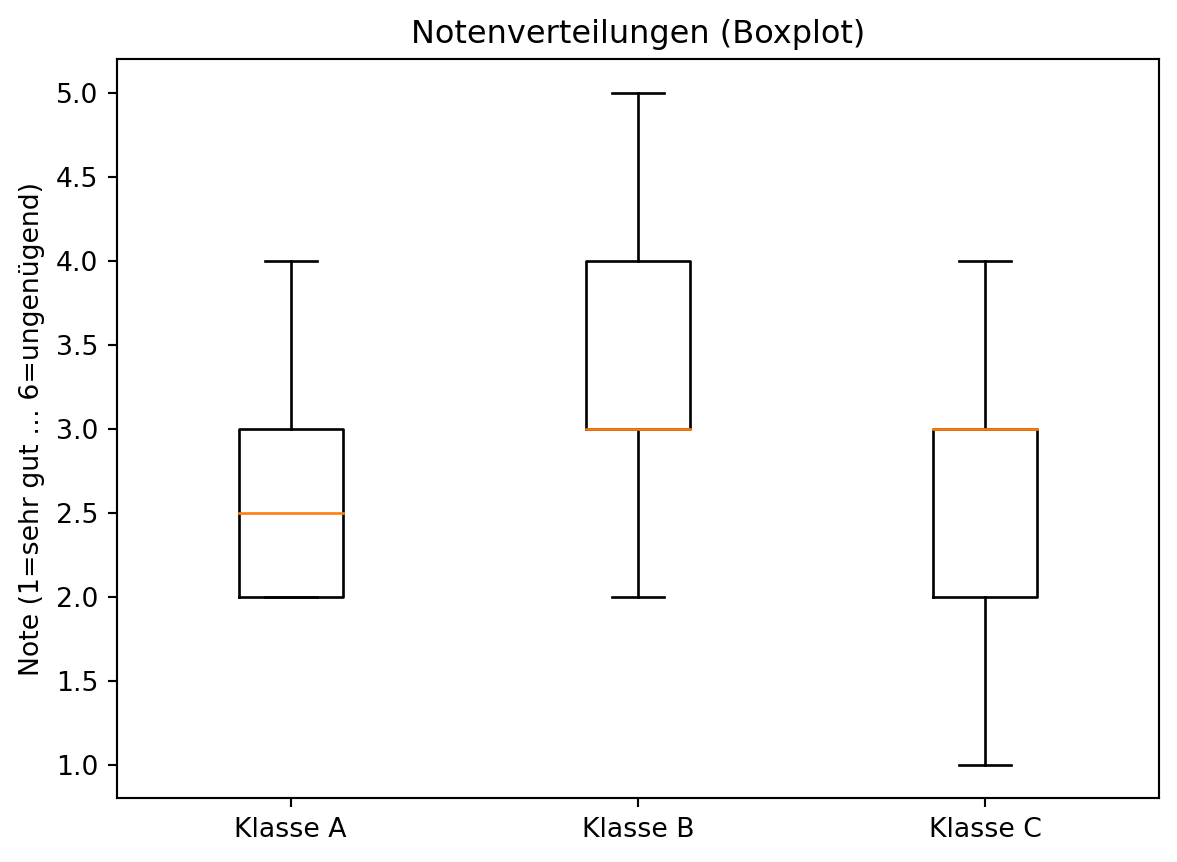
• Boxplot (Kastendiagramm):
  Fasst die Verteilung einer metrischen Variablen durch Median, Quartile und Ausreißer zusammen.
  Besonders nützlich zum Vergleich mehrerer Gruppen.

  Beispiel: Notenverteilungen verschiedener Klassen.

  

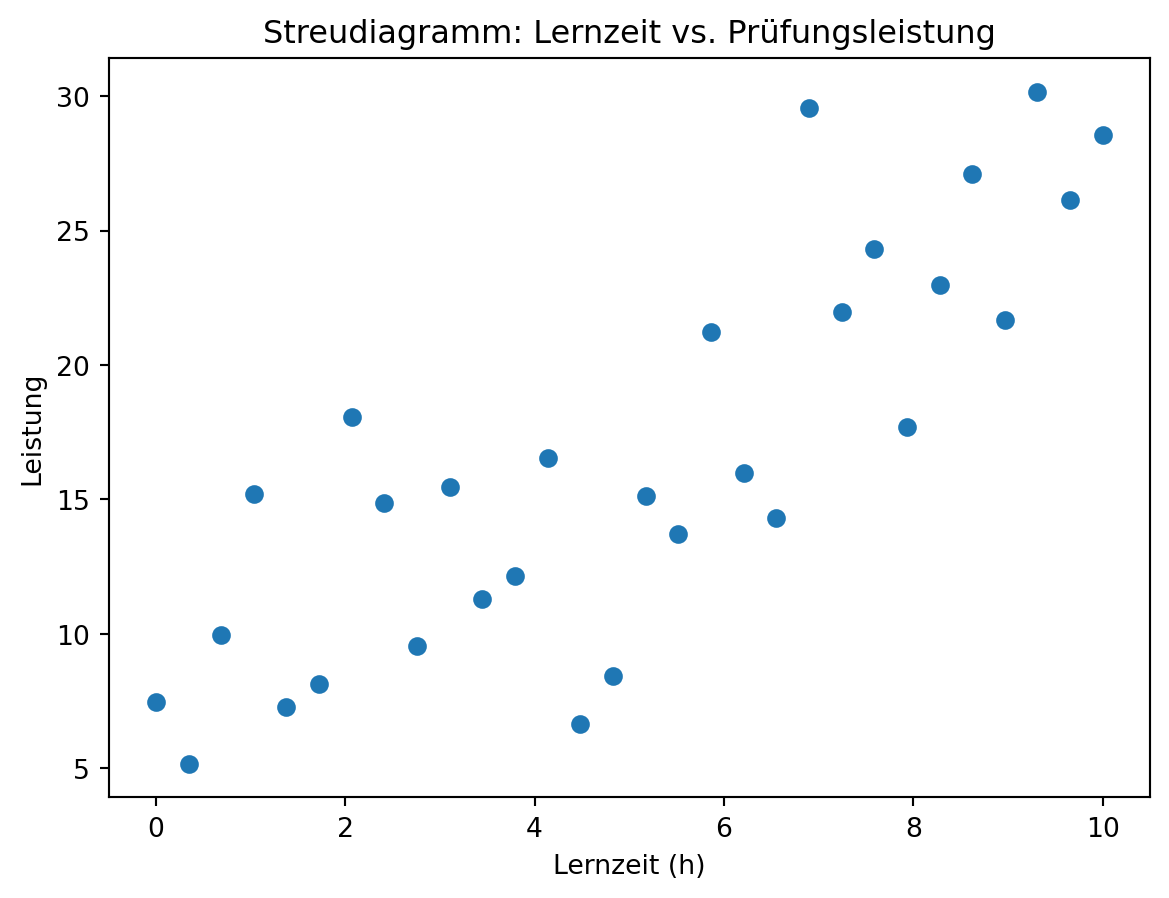
• Streudiagramm (Scatter Plot):
  Zeigt den Zusammenhang zwischen zwei metrischen Variablen.
  Jedes Datenpaar wird als Punkt im Koordinatensystem dargestellt.

  Beispiel: Zusammenhang zwischen Lernzeit und Prüfungsergebnis.

  

Zeitliche Entwicklungen

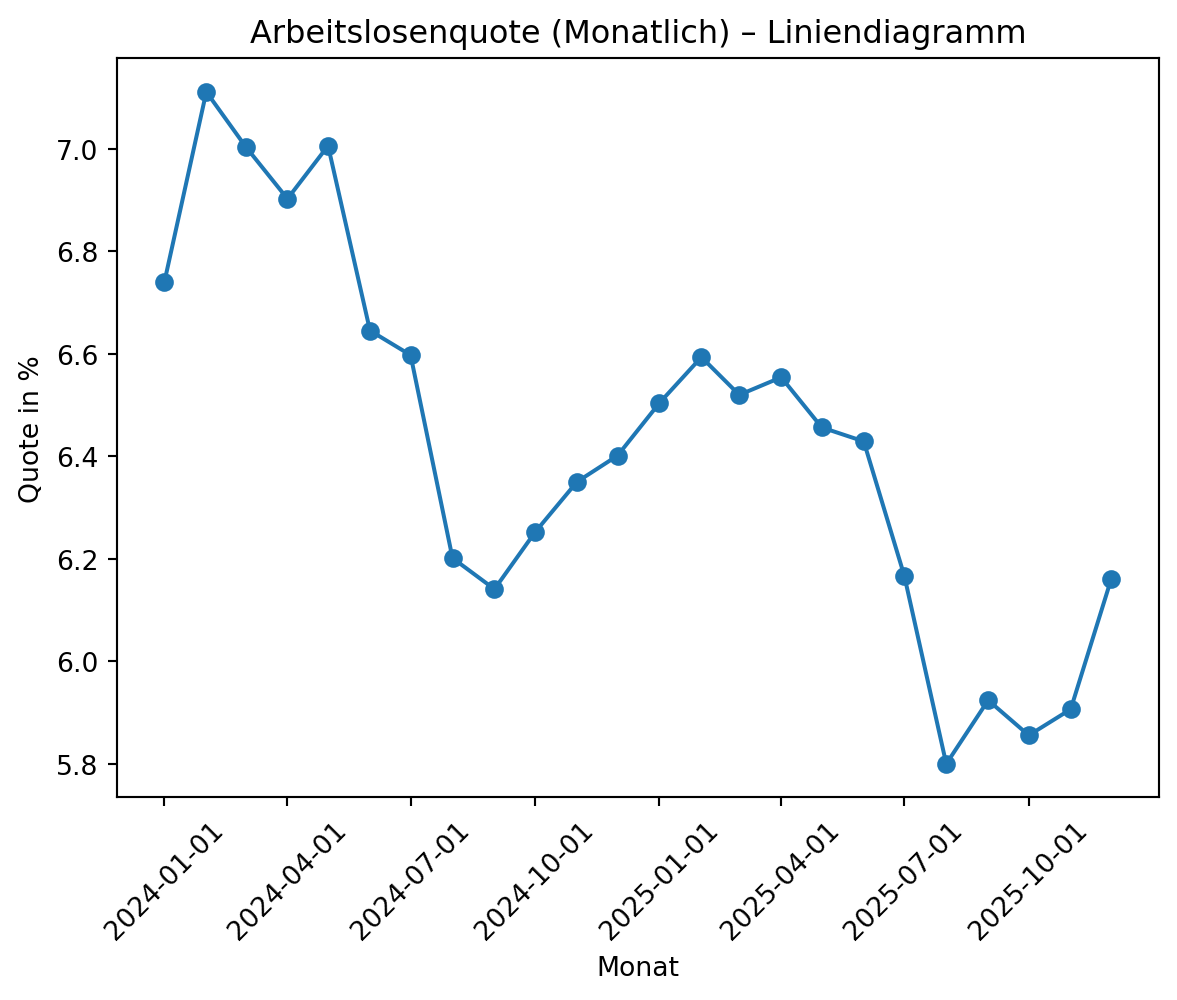
• Liniendiagramm:
  Eignet sich für Zeitreihen, da es den Verlauf einer Variable über die Zeit zeigt.
  Mehrere Linien ermöglichen den Vergleich verschiedener Gruppen.

  Beispiel: Entwicklung der Arbeitslosenquote über die letzten 10 Jahre.